Generalized dessins — Part 3: operations on dessins, profinite free groups
This post assumes you have read Part 1 and Part 2!
In this blog post, we discuss various operations that one can apply to dessins. We also relate dessins to subgroups of profinite free groups.
operations on dessins
degeneracy
Consider an \(n\)-dessin \(\D = (V_i, E, s_i)\). Add a color somewhere in the order of colors (at the \(i\)-th position), and add to each hyperedge a different vertex of this color. In this way, one obtains an \((n+1)\)-dessin.
Definition (degeneracy): The (\(i\)-th) degeneracy of the \(n\)-dessin \(\D\) is the \((n+1)\)-dessin constructed above.
The degeneracy operation defines, for every \(i \in \{0,\ldots,n\}\)), an embedding (faithful functor) \(D_i\) from the category of \(n\)-dessins into the category of \((n+1)\)-dessins.
Example:
We turn a dessin d’enfant into a \(3\)-dessin by adding the color green:
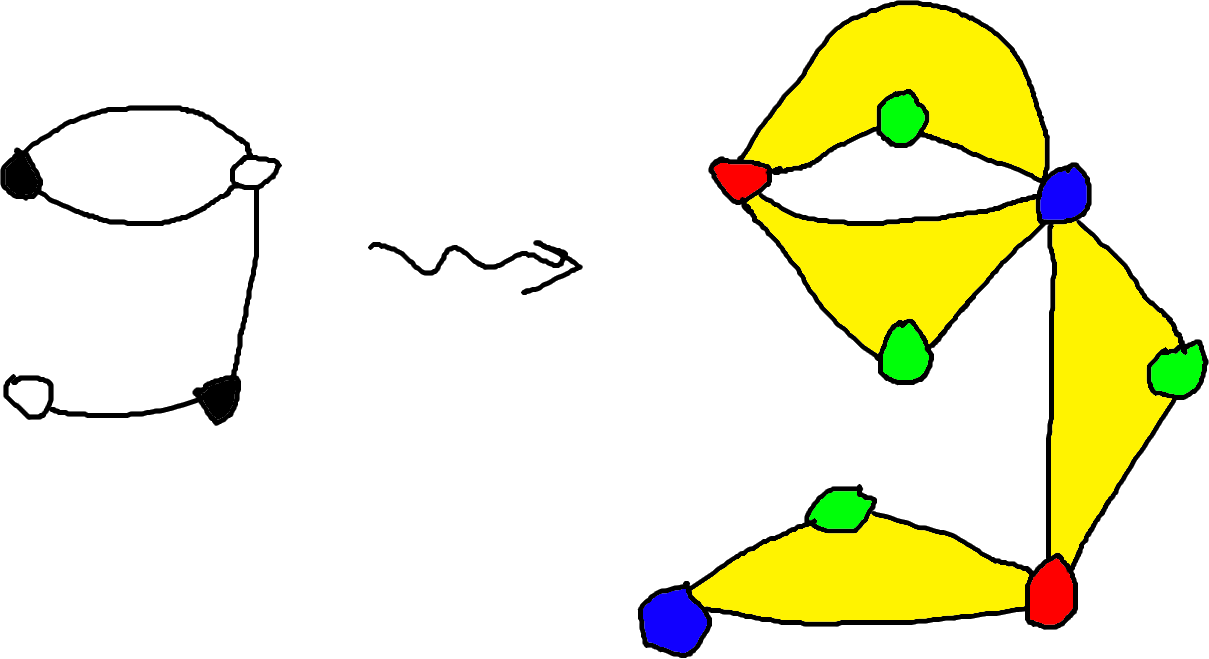
In terms of monodromy elements (i.e. branch cycle description), this operation transforms the \(n\)-tuple:
\[(g_1, \ldots, g_n)\]into the \((n+1)\)-tuple:
\[(g_1, \ldots, g_i, 1, g_{i+1}, \ldots, g_n).\]In terms of covers of the projective line, this operation adds a new “branch point” at which the cover is not actually branched.
Remark: Denote by \(\Dess_{n,E}\) the category of \(n\)-dessins (or clean \(n\)-dessins) whose set of hyperedges is \(E\). We have defined, for \(i \in \{0,\ldots,n\}\), embeddings \(D_i : \Dess_{n,E} \to \Dess_{n+1,E}\). For \(i \in \{1, \ldots, n-1\}\), we can also define a surjective functor \(S_i : \Dess_{n,E} \to \Dess_{n-1,E}\) by the formula:
\[(g_1,\ldots, g_n) \mapsto (g_1, \ldots, g_i g_{i+1}, g_{i+2}, \ldots, g_n).\]This operation is harder to describe geometrically. Using these functors as degeneracy/face morphisms, we equip the set of all dessins (or all clean dessins) with the strucure of a simplicial category (a simplicial object in \(\Cat\)). In the case of clean dessins, the underlying simplicial set is connected (there is a single vertex) and it has the homotopy type of an Eilenberg-Maclane space \(K(\Sym_E,1)\).
concatenation
Consider two dessins whose set of hyperedges is a common given set \(E\). Namely, take an \(n\)-dessin \(\D = \left(V^{(1)}_i, E, s^{(1)}_i\right)\) and an \(n'\)-dessin \(\D' = \left(V^{(2)}_i, E, s^{(2)}_i\right)\).
The following family of maps:
\[s_i(e) = \left\lbrace \begin{matrix} s^{(1)}_i(e) & \text{ if } & i \in \{1,\ldots,n\} \\ s^{(2)}_{i-n}(e) & \text{ if } & i \in \{n+1,\ldots,n+n'\} \end{matrix} \right. \,\,\, ,\]defines an \((n+n')\)-dessin:
\[\mathcal{DD'} = \Bigg( \left( V^{(1)}_1, \ldots, V^{(1)}_n, V^{(2)}_1, \ldots, V^{(2)}_{n'} \right) ,\, E ,\, s_i \Bigg) \, .\]Definition (concatenation): The concatenation of the dessins \(\D\) and \(\D'\) is the \((n+n')\)-dessin \(\mathcal{DD'}\) constructed above.
The monodromy group of the concatenated dessin is the subgroup of \(\Sym_E\) generated by the monodromy groups of \(\D\) and \(\D'\). The concatenation of two clean dessins is itself a clean dessin.
Example: We glue the two following dessins d’enfants (note that one of them is degenerate):
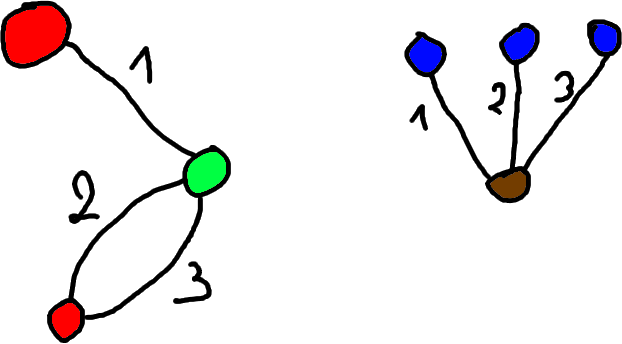
We obtain the following degenerate \(4\)-dessin:
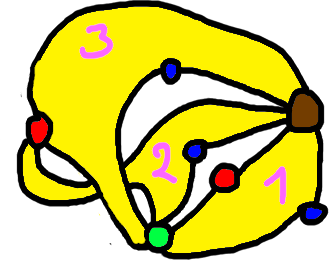
Note that the genus increased (both initial dessins d’enfants were genus \(0\), the glued \(4\)-dessin is genus \(1\)).
In general, gluing two dessins of respective genus \(g_1\) and \(g_2\) gives a dessin of genus at most \(g_1 + g_2 - 1 + \card{E}\). If at least one of the original dessins is clean, this is an equality.
Note that degeneracy is a particular case of concatenation, with the \(1\)-dessin having exactly one “edge” around each of the \(\card{E}\) vertices.
braid group action (aka Hurwitz action)
We start by focusing on the case of dessins d’enfants (\(n=2\)).
We describe an action of the braid group \(\B_n\) on dessins; this action corresponds to moving on a Hurwitz space (moduli space of covers). We give a graphical interpretation the action of the braid that swaps the branch points \(\bullet\) and \(\circ\) by rotating counterclockwise:
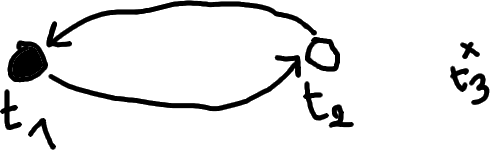
In terms of monodromy elements, the corresponding operation is simply:
\[(g_1, g_2, (g_1g_2)^{-1}) \mapsto (g_2, g_2^{-1} g_1 g_2, (g_1g_2)^{-1}).\]Note that this operation does not change the monodromy group, and maps clean dessins to clean dessins.
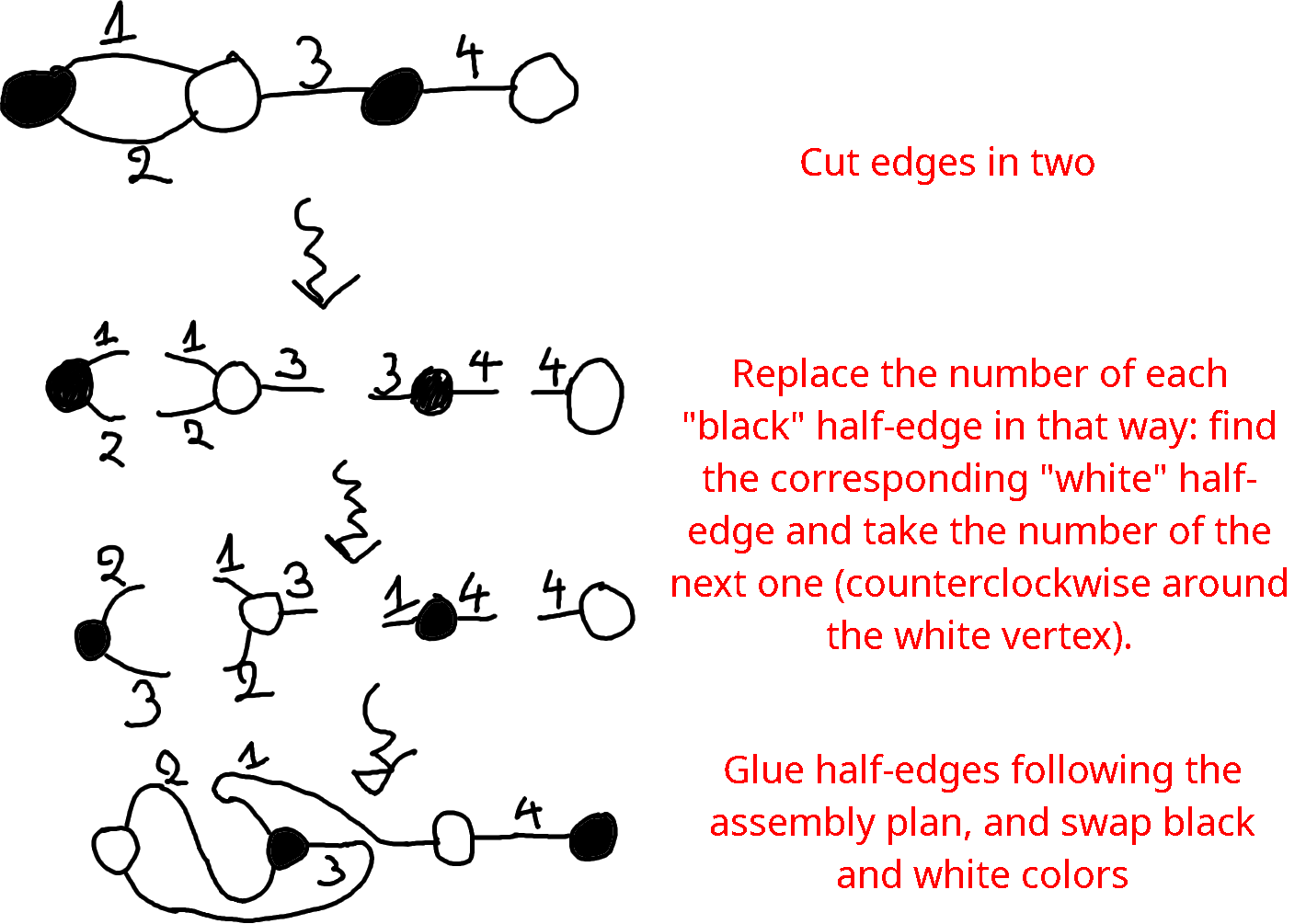
To graphically apply this operation to a dessin, follow these steps:
- Cut every edge in two: then there are black and white vertices surrounded by “half-edges”
- Connect each half-edge surrounding a black vertex to the white vertex that it was previously connected to, but not to the same half-edge: instead, connect it to the next half-edge when rotating positively around that white vertex
- Once done, swap the colors black and white.
Example:
When there are more colors, here is how elementary braids are to be understood: Pick two colors, consecutive in the cyclical order \((1, 2 \cdots, n)\). Cut from each hyperedge the corner corresponding to the first color. Glue each cut corner to the hyperedge following (for the second color) the hyperedge that corner was cut from. Finally, swap the two colors.
We do not give a graphical interpretation to braids involving the point \(t_{n+1}\). One way to deal with them is: clean the dessin, act on the cleaned dessin, and then remove all vertices with the “additional” color.
dessins and profinite free groups
In what follows, we denote by \(\sigma_1, \ldots, \sigma_n\) the standard generators (letters) of the free group \(F_n\). Note that we can (and sometimes do) see \(F_n\) as being generated by \(n+1\) letters \(\sigma_1, \ldots, \sigma_{n+1}\) satisfying the generating relation \(\sigma_1 \cdots \sigma_{n+1} = 1\).
dessins as subgroups of (profinite) free groups
Proposition: There is a natural bijection between conjugacy classes of subgroups of finite index of \(F_n\) and isomorphism classes of connected \(n\)-dessins.
Through this correspondance, regular dessins correspond to normal subgroups of finite index of \(F_n\) (or, equivalently, open subgroups of \(\hat F_n\)): in that case, that normal subgroup is the kernel of the monodromy morphism \(F_n \to \Sym_E\) (mapping the \(i\)-th letter to the \(i\)-th monodromy element). The regular closure of an \(n\)-dessin is given by the normal closure of the corresponding conjugacy class of subgroups. The quotient of \(F_n\) by the normal closure is isomorphic to the monodromy group of the dessin.
We now give a few details concerning the construction that leads to the proposition above:
Proof: Take a connected \(n\)-dessin \(\D\). Denote by \(p\) the surjective morphism \(F_n \to \hat{\D}\) taking the \(i\)-th letter to the \(i\)-th monodromy element of \(\D\). Consider a hyperedge \(e \in E\), and define the following subgroup of \(F_n\):
\[K_e = \{ g \in F_n \mid p(g).e = e \}.\]If \(e' \in E\) is another hyperedge, and \(\gamma \in \hat{\D}\) is such that \(e' = \gamma.e\) (which is possible since \(\D\) is connected), and \(\tilde \gamma\) is any lift of \(\gamma\) in \(F_n\), then we have \(K_e = K_{e'}^{\tilde\gamma}\). Thus we have associated to the \(n\)-dessin \(\D\) a well-defined conjugacy class of subgroups of \(F_n\), which is independent of the choice of a base-hyperedge.
Conversely, consider a conjugacy class of subgroups of finite index of \(F_n\), from which you pick a representative \(K \subseteq F_n\). We define an \(n\)-dessin in the following way:
-
The set \(E\) of hyperedges consists of one representative from each left coset of \(F_n\) modulo \(K\):
\[E = \{g_1, \ldots, g_d\}\] \[F_n = g_1K \sqcup g_2K \sqcup \ldots \sqcup g_dK\] - The permutation \(\sigma_i \in \Sym_E\) is defined in the following way: the hyperedge \(g_j\) is mapped to the representative in \(E\) of the left coset of \(\sigma_i g_j \in F_n\) modulo \(K\).
- The set \(V_i\) of vertices of color \(i\) consists of all cycles in the cycle decomposition of \(\sigma_i\). The map \(s_i : E \to V_i\) takes each hyperedge to the cycle that contains it in \(\sigma_i\), and the cyclical order on \(s_i^{-1}(v)\) (for some vertex \(v \in V_i\)) is the corresponding cycle in \(\sigma_i\).
These two constructions are quasi-inverse. All details are left as exercise for the reader. ■
The subgroup \(K_e\), where \(e\) is a base-hyperedge, is isomorphic to the fundamental group of the cover describe by the \(n\)-dessin \(\D\). In particuliar, it is a free group whose rank is equal to twice the genus of the surface (which we have computed in part 1):
\[2-\sum\card{V_i} - (1-n)\card{E} + \kappa.\]degeneracy in terms of free groups
Let \(i \in \{0,\ldots,n\}\). We define a continuous surjective morphism \(\hat F_{n+1} \twoheadrightarrow \hat F_n\): \(\delta_{i,n} : \sigma_j \mapsto \left\lbrace \begin{matrix} \sigma_j & \text{if} & j \leq i \\ 1 & \text{if} & j = i + 1 \\ \sigma_{j-1} & \text{if} & j > i + 1 \end{matrix} \right.\)
The kernel of \(\delta_{i,n}\) is the normal closed subgroup of \(\hat F_{n+1}\) topologically generated by \(\sigma_{i+1}\). If \(U\) is a subgroup of \(\hat F_n\) of finite index \(d\), then the subgroup \(\delta_{i,n}^{-1}(U)\) of \(\hat F_{n+1}\) is also of index \(d\). This is a translation of the degeneracy operation in the language of subgroups of profinite free groups.
various lemmas on profinite free groups
These lemmas, concerning profinite free groups, will be useful in later parts.
Lemma: The abelianization of \(\hat F_n\), i.e. its quotient by the closed subgroup \([\hat F_n, \hat F_n]\) topologically generated by commutators, is \(\hat \Z^n\).
Definition (multiplicity of a letter): The multiplicities in an element \(x \in \hat F_n\) are the profinite integers \(m_1(x), \ldots, m_n(x) \in \hat \Z\) such that:
\[x = \sigma_1^{m_1(x)}\cdots\sigma_n^{m_n(x)} \mod [\hat F_n, \hat F_n].\]We moreover define \(m_{n+1}(x) = - \sum_{i=1}^n m_i(x)\), so that \(\sum_{i=1}^{n+1} m_i(x) = 0\). We say that \(m_i(x)\) is the multiplicity of the \(i\)-th letter \(\sigma_i\) in \(x\).
Lemma: If \(x \in \hat F_n\) commutes with the \(i\)-th letter \(\sigma_i\), then there exists a profinite integer \(u \in \hat \Z\) such that \(x = \sigma_i^u\).
This lemma follows from Theorem B in Torsion elements and centralizers in free products of profinite groups by Wolfgang Herfort and Luis Ribes (J. Reine Angew. Math. 358 (1985), pp. 155–161), applied to the following situation: \(A\) is topologically generated by the letter \(\sigma_i\), \(B\) is topologically generated by all other letters (\(\sigma_j, j\neq i\)), and \(a\) is the letter \(\sigma_i\).
Lemma: Every group automorphism of a topologically finitely generated profinite group (in particular a profinite free group of finite rank) is continuous.
This lemma follows from Finite index subgroups in profinite groups by Nikolay Nikolov and Dan Segal (Comptes Rendus de l’Académie des Sciences, Paris, Ser. I 337 (2003)) [link to preprint].
In the next blog post, we will discuss the Galois action(s) on dessins and its description.